Jump to part:
1 - 2 - 3 - 4 - 5
API

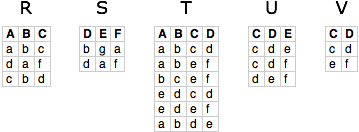
an introduction to ratcl - Part 2

With the basics out of the way, it's time to go into some more substantial data manipulations. First, some demo data:

These create the following views:

The examples below all use "functional operations" returning a new view without altering the input views. All the above views retain their original content.

Selection of a view can be done through a "row map", i.e. a list of row numbers to keep:

Similarly, a column map can be used to extract a number of columns:

Projection returns a view with only the columns specified, and no duplicate rows:

Here's the cross-product:

Two variants of relational join:

Relational join is a workhorse for many purposes, the above "join1" drops unmatched rows, while "join0" returns rows which did not match in the join.

Division is also a (lesser used) core operator of relational algebra:

Set operations

Set operations are straightforward. They take two views and return a new one:

The input views must be sets, i.e. contain no duplicate rows. If this is not the case, the "unique" operator can be used to produce a proper set:

This example shows that mapcol + unique is equivalent to a projection.

All views used for set operations must (for now) also have the same columns in the same order. This can be enforced through "mapcol" or "project".

Applying set operations on anything else leads to (as yet) undefined results.

no iteration

As you can see, relational algebra offers a way to manipulate structured collections of data in quite a few ways, without dealing with details of any implied iterations. Ratcl helps you think in terms of high-level transformations.

The next page describes one more important operator of relational algebra.

Continued...

Copyright � 2020 Equi4 Software. Metakit is a trademark of Equi4 Software.